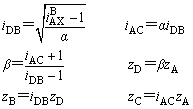NW型传动配齿方法及齿数组合表
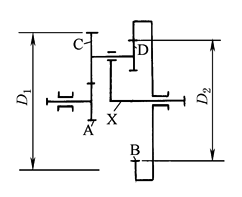
图1									NW型传动通常取zA、zB为行星轮数目Cs的整数倍。常用传动方式为B轮固定，A轮主动，行星架输出。为获得较大传动比和较小外形尺寸，应选择zA、zD均小于zC。为使齿轮接近等强度，zC与zD之值相差越小越好。综合考虑，一般取zD＝zC-(3~8)为宜 在NW传动中，若所有齿轮的模数及齿形角相同，且zA+zC＝zB-zD，则由同心条件可知，其啮合角α'tAC＝α'tBD。为了提高齿轮承载能力，可使两啮合角稍大于20°，以便A、D两轮进行正变位。选择齿数时，取zA+zC＜zB-zD，但zB会因此增大，从而导致传动的外廓尺寸加大
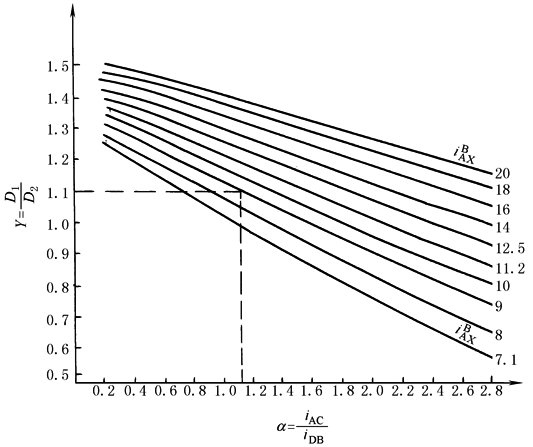
NW型传动按下列步骤配齿 ① 根据强度、运转平稳性和避免根切等条件确定太阳轮齿数zA，常取zA为Cs的倍数 ② 根据结构设计对两对齿轮副径向轮廓尺寸比值D1/D2(图1)的要求拟定Y值，再由传动比和Y值查图2确定系数α，然后，按下列 各式计算iDB、iAC、β值和齿数zD、zB、zC 图2  根据和确定的线图 ③ 根据算出的齿数，按前述装配条件的两个限制条件对其进行调整并确定zD、zB和zC。为了使确定的齿数仍能满足同心条件，可以将其中一个行星轮的齿数zC留在最后确定，在确定该齿数zC时，要同时考虑同心条件，即对于非角变位齿轮传动： zC＝zSAC-zA或zD＝zB-zSΑC 对不等啮合角的角变位传动： zC＝zSAC-zA-Δz或zD＝zB-zSAC-Δz zSAC＝zA+zC 式中　Δz——角变位要求行星轮C或D应减少的齿数，一般取Δz＝1~2 ④ 校核传动比，同时根据表确定齿数应满足的条件中表校核邻接条件
NW型行星齿轮传动常用传动比对应的齿轮齿数组合见表
Cs＝3的NW型行星传动的齿数组合
	zA	zB	zC	zD		zA	zB	zC		zD		zA	zB	zC	zD		zA	zB	zC	zD
7.000	21	63	28	14	7.857	18	108	48		42	8.821	18	111	52	41	11.880	21	102	56	25
7.000	12	54	24	18	7.867	18	111	49		44	8.824	12	57	28	17	·12.071	15	99	52	31
7.000	18	60	27	15	7.871	21	78	37		20	8.826	18	81	40	23	·12.131	18	102	55	28
7.000	18	81	36	27	·7.878	18	108	47		41	8.835	21	93	46	26	12.163	12	81	43	26
7.041	21	111	48	42	·7.888	15	87	38		32	·8.839	18	93	44	29	12.273	21	99	55	23
7.045	21	114	49	44	7.890	15	81	37		29	·8.845	12	78	35	29	12.284	15	99	53	31
7.053	21	105	46	38	·7.897	12	75	32		29	8.846	12	72	34	26	12.333	18	102	56	28
·7.055	21	87	38	26	7.905	15	96	41		38	8.846	18	108	51	39	12.371	12	90	47	31
·7.058	18	81	35	26	7.915	18	117	50		47	·8.892	15	81	38	26	12.500	12	87	46	29
·7.059	21	111	47	41	·7.936	21	96	44		29	8.895	18	108	50	38	12.529	15	105	56	34
7.071	21	102	45	36	7.943	18	93	43		32	8.906	12	69	33	24	·12.610	12	81	43	25
·7.088	12	54	23	17	7.957	21	84	40		23	8.933	18	102	49	35	12.667	18	105	58	29
7.097	15	78	34	29	7.971	18	78	37		23	8.965	21	99	49	29	12.688	15	102	55	32
·7.106	21	102	44	35	·7.982	12	51	23		14	8.994	18	87	43	26	·12.786	21	99	55	22
7.109	15	84	36	33	8.000	21	105	49		35	·9.000	12	69	32	23	12.867	12	93	49	32
7.111	15	75	33	27	·8.000	15	78	35		26	9.000	18	99	48	33	12.880	12	81	44	25
7.111	18	66	30	18	8.000	15	63	30		18	9.063	15	90	43	32	·13.115	12	84	45	26
·7.118	15	60	26	17	8.000	18	90	42		30	9.067	15	66	33	18	13.248	21	102	58	23
·7.125	15	84	35	32	8.028	18	69	33		18	9.100	12	54	27	15	13.284	15	102	56	31
7.143	21	96	43	32	·8.057	15	57	26		14	9.120	15	87	42	30	13.292	18	105	59	28
·7.154	15	75	32	26	8.065	21	102	48		33	9.138	12	63	31	20	·13.460	21	102	59	23
7.159	18	75	34	23	·8.069	18	90	41		29	9.195	18	93	46	29	13.517	15	99	55	29
·7.190	18	60	26	14	8.088	21	90	43		26	·9.200	15	87	41	29	13.641	18	102	58	26
7.200	15	69	31	23	8.125	12	57	27		18	9.211	18	108	52	38	·13.650	15	102	55	31
7.200	21	93	42	30	·8.134	21	102	47		32	9.229	15	72	36	21	13.672	12	90	49	29
7.205	21	81	37	23	8.143	18	75	36		21	9.264	18	105	51	36	13.688	15	105	58	32
7.222	18	96	42	36	·8.165	15	63	29		17	·9.282	15	66	32	17	·13.805	21	102	58	22
7.224	18	99	43	38	8.171	18	108	49		41	9.293	12	78	37	29	13.880	12	84	46	25
·7.248	18	96	41	35	8.178	18	114	51		45	9.308	15	81	40	26	13.897	15	111	61	35
7.250	18	90	40	32	8.179	18	105	48		39	9.323	18	90	45	27	·14.000	12	96	52	32
7.250	18	105	45	42	·8.215	18	105	47		38	9.330	12	60	30	18	·14.097	15	105	58	31
·7.255	18	66	29	17	·8.216	18	69	32		17	·9.333	18	105	50	35	·14.147	18	102	58	25
·7.260	18	105	44	41	8.229	15	69	33		21	9.333	12	75	36	27	14.200	15	99	56	28
·7.261	21	93	41	29	8.233	15	93	42		36	·9.357	12	54	26	14	·14.276	15	111	61	34
7.283	18	87	39	30	8.242	15	96	43		38	·9.400	15	72	35	20	14.323	15	105	59	31
7.286	18	72	33	21	8.251	21	96	46		29	·9.413	12	75	35	26	14.373	18	102	59	25
7.286	21	72	33	18	·8.263	15	93	41		35	9.422	18	99	49	32	14.494	15	111	62	34
7.286	15	66	30	21	·8.265	12	57	26		17	9.450	15	78	39	24	14.500	12	99	54	33
7.317	21	111	49	41	8.273	18	96	45		33	·9.462	18	90	44	26	14.600	15	102	58	29
7.330	21	108	48	39	8.280	15	84	39		30	9.500	12	69	34	23	·14.630	18	99	57	23
·7.361	21	108	47	38	·8.292	18	75	35		20	·9.529	12	60	29	17	14.663	12	87	49	26
7.367	21	78	36	21	8.313	18	81	39		24	9.533	18	96	48	30	14.686	18	105	61	26
7.374	21	87	40	26	8.328	12	75	34		29	·9.591	15	78	38	23	·15.086	15	102	58	28
·7.380	15	66	29	20	·8.333	18	96	44		32	9.600	15	87	43	29	15.329	15	102	59	28
7.384	21	102	46	35	8.333	12	72	33		27	9.643	12	66	33	21	15.467	18	105	62	25
7.404	18	81	37	26	·8.338	15	84	38		29	9.644	18	96	47	29	15.723	15	99	58	26
·7.413	12	69	29	26	·8.360	15	69	32		20	9.667	18	105	52	35	15.724	15	105	61	29
7.429	15	54	25	14	8.364	12	81	36		33	9.711	15	84	42	27	15.800	15	111	64	32
7.429	21	99	45	33	·8.383	12	81	35		32	9.758	18	102	51	33	15.849	12	111	61	38
7.475	15	84	37	32	8.400	15	78	37		26	9.800	15	62	34	17	16.029	18	102	61	23
·7.482	21	99	44	32	8.413	12	66	31		23	·9.800	12	66	32	20	·16.250	15	105	61	28
·7.500	21	78	35	20	8.414	18	90	43		29	·9.831	15	84	41	26	·16.250	12	111	61	37
7.500	15	90	39	36	·8.435	18	81	38		23	9.846	18	90	46	26	·16.277	15	111	64	31
7.500	21	84	39	24	8.438	21	102	49		32	·9.854	18	102	50	32	·16.312	15	99	58	25
7.500	18	78	36	24	8.485	18	114	52		44	·9.880	15	72	37	20	16.500	15	105	62	28
·7.514	15	90	38	35	8.488	18	111	51		42	·9.894	12	75	37	26	16.500	12	111	62	37
7.538	15	75	34	26	8.500	12	63	30		21	10.000	12	54	28	14	16.516	15	111	65	31
7.552	18	96	43	35	8.519	18	87	42		27	10.043	15	78	40	23	16.712	18	102	61	22
7.563	12	45	21	12	·8.520	18	111	50		41	10.118	12	60	31	17	16.954	15	102	61	26
7.567	21	93	43	29	8.522	18	105	49		36	10.310	12	81	40	29	17.232	18	105	64	23
7.576	18	93	42	33	8.543	21	99	48		30	·10.512	15	99	49	34	·17.457	15	108	64	28
7.578	18	111	42	45	8.556	18	102	48		36	10.625	12	63	33	18	·17.592	15	102	61	25
·7.587	18	111	47	44	8.600	15	57	28		14	10.706	15	99	50	34	17.714	15	108	65	28
·7.594	18	78	35	23	·8.609	15	75	35		23	·10.838	15	105	52	37	17.864	15	102	62	25
·7.609	21	84	38	23	8.610	18	102	47		35	10.857	12	69	36	21	17.914	12	111	64	35
·7.620	18	93	41	32	·8.613	12	63	29		20	·10.882	12	63	32	17	18.097	15	111	67	29
7.632	21	108	40	38	8.617	15	93	43		35	10.884	12	81	41	28	·18.179	12	111	65	35
7.667	18	60	28	14	·8.622	18	87	41		26	11.000	12	78	40	26	18.231	15	105	64	26
7.667	18	87	40	29	8.636	15	90	42		33	11.027	15	105	53	37	·18.333	15	108	65	27
7.686	18	66	31	17	·8.640	21	99	47		29	11.103	15	102	52	35	·18.412	12	111	64	34
·7.714	21	105	47	35	8.659	15	63	31		17	·11.349	18	105	55	31	·18.707	15	111	67	28
·7.758	21	90	41	26	8.667	18	69	34		17	11.400	15	102	52	34	18.879	12	102	61	29
7.769	12	45	20	13	·8.688	15	90	41		32	11.500	12	63	34	17	·19.518	12	102	61	28
7.777	21	99	46	32	8.708	18	75	37		20	11.538	18	105	56	31	19.821	12	102	62	28
7.800	18	72	34	20	8.724	15	84	40		29	·11.552	18	102	54	29	20.367	12	111	67	32
7.800	12	51	24	15	8.750	18	93	45		30	11.600	15	102	53	34	·20.992	12	111	67	31
7.820	15	60	31	20	8.800	15	81	39		27	11.638	12	69	37	20	21.290	12	111	68	31
7.856	12	69	31	26	8.800	12	73	36		30	11.725	15	99	52	32	21.923	12	102	64	26
7.857	15	90	40	35	8.805	12	81	37		32	11.747	18	102	55	29
注：1．本表zA及zB都是3的倍数，适用于Cs＝3的行星传动。个别组的zA、zB也同时是2的倍数，也可适用于Cs＝2的行星传动。 2．带“·”记号者，zA+zC≠zB-zD，用于角变位传动；不带“·”者，zA+zC＝zB-zD，可用于高变位或非变位传动。 3．当齿数小于17且不允许根切时，应进行变位。 4．表中同一个而对应有几个齿数组合时，则应根据齿轮强度选择。 5．表中齿数系按模数mtA＝mtB条件列出。