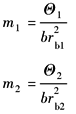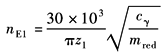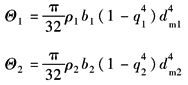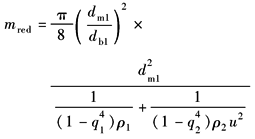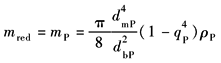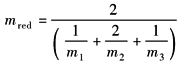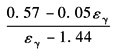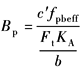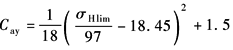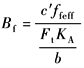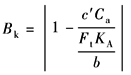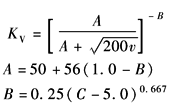|
动载系数KV |
|||||||||||||||||||||
|
动载系数KV是考虑齿轮制造精度、运转速度对轮齿内部附加动载荷影响的系数,定义为
影响动载系数的主要因素有:由基节和齿廓偏差产生的传动误差;节线速度;转动件的惯量和刚度;轮齿载荷;轮齿啮合刚度在啮合循环中的变化。其他的影响因素还有:跑合效果、润滑油特性、轴承及箱体支承刚度及动平衡精度等 在通过实测或对所有影响因素作全面的动力学分析来确定包括内部动载荷在内的最大切向载荷时,可取KV等于1。不能实现时,可用下述方法之一计算动载系数 ① 一般方法 KV的计算公式见表1 |
|||||||||||||||||||||
|
表1 运行转速区间及其动载系数KV的计算公式 |
|||||||||||||||||||||
|
运行转 速区间 |
临界转速比 N |
对运行的齿轮 装置的要求 |
KV计算公式 |
备注 |
|||||||||||||||||
|
亚临界区 |
N≤Ns |
多数通用齿轮在此区工作 |
KV=NK+1 =N(CV1Bp+CV2Bf+CV3Bk)+1 (1) |
在N=1/2或2/3时可能出现共振现象,KV大大超过计算值,直齿轮尤甚。此时应修改设计。在N=1/4或1/5时共振影响很小 |
|||||||||||||||||
|
主共振区 |
Ns<N≤1.15 |
一般精度不高的齿轮(尤其是未修缘的直齿轮)不宜在此区运行。εγ>2的高精度斜齿轮可在此区工作 |
KV=CV1Bp+CV2Bf+CV4Bk+1 (2) |
在此区内KV受阻尼影响极大,实际动载与按式(2)计算所得值相差可达40%,尤其是对未修缘的直齿轮 |
|||||||||||||||||
|
过渡区 |
1.15<N<1.5 |
|
(3) |
KV(N=1.5)按式(4)计算 KV(N=1.15)按式(2)计算 |
|||||||||||||||||
|
超临界区 |
N≥1.5 |
绝大多数透平齿轮及其他高速齿轮在此区工作 |
KV=CV5Bp+CV6Bf+CV7 (4) |
1.可能在N=2或3时出现共振,但影响不大 2.当轴齿轮系统的横向振动固有频率与运行的啮合频率接近或相等时,实际动载与按式(4)计算所得值可相差100%,应避免此情况 |
|||||||||||||||||
|
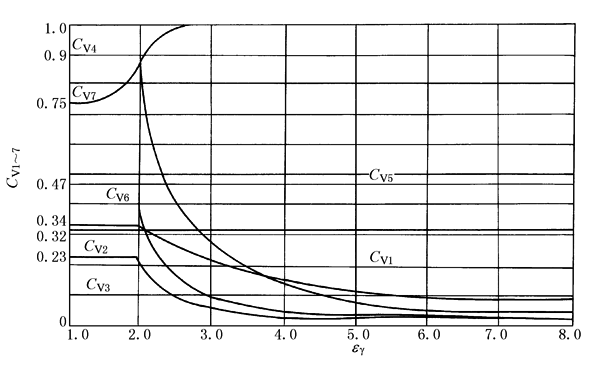
注:1.表中各式均将每一齿轮副按单级传动处理,略去多级传动的其他各级的影响。非刚性连接的同轴齿轮,可以这样简化,否则应按表4中第2类型情况处理。 2.亚临界区中当(FtKA)/b<100N/mm时, 3.表内各式中: N—临界转速比,见表2; CV1—考虑齿距偏差的影响系数; CV2—考虑齿廓偏差的影响系数; CV3—考虑啮合刚度周期变化的影响系数; CV4—考虑啮合刚度周期性变化引起齿轮副扭转共振的影响系数; CV5—在超临界区内考虑齿距偏差的影响系数; CV6—在超临界区内考虑齿廓偏差的影响系数; CV7—考虑因啮合刚度的变动,在恒速运行时与轮齿弯曲变形产生的分力有关的系数; Bp、Bf、Bk—分别考虑齿距偏差、齿廓偏差和轮齿修缘对动载荷影响的无量纲参数。其计算公式见表6 CV1~CV7按表5的相应公式计算或由图1查取 |
|||||||||||||||||||||
|
表2 临界转速比N |
|||||||||||||||||||||
|
项目 |
单位 |
计 算 公 式 |
项 目 |
单位 |
计 算 公 式 |
||||||||||||||||
|
临界转 速比 |
|
|
小、大轮转化到啮合线上的单位齿宽当量质量 |
kg/mm |
|
||||||||||||||||
|
临界转速 |
r/min |
cγ——齿轮啮合刚度,N/(mm·μm),见表轮齿刚度 |
转动惯量 |
kg·mm2 |
|
||||||||||||||||
|
诱导质量 |
kg/mm |
对一般外啮合传动
ρ1、ρ2——齿轮材料密度,kg/mm3 对行星传动和其他较特殊的齿轮,其mred见表3和表4 |
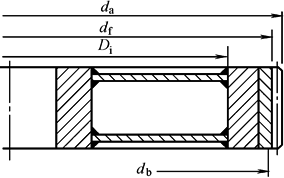
平均直径 |
mm |
|
||||||||||||||||
|
轮缘内腔直径与平均直径比 |
|
|
|||||||||||||||||||
|
表3 行星传动齿轮的诱导质量mred |
|||||||||||||||||||||
|
齿轮组合 |
mred计算公式或提示 |
备注 |
|||||||||||||||||||
|
太阳轮(S)| 行星轮(P) |
|
nP——轮系的行星轮数 mS,mP——太阳轮、行星轮的当量质量,可用表2中求小、大齿轮当量质量的公式计算 |
|||||||||||||||||||
|
行星轮(P)| 固定内齿圈 |
|
把内齿圈质量视为无穷大处理 ρP——行星轮材料密度 dm,db,q定义及计算参见表2及表中图 |
|||||||||||||||||||
|
行星轮(P)| 转动内齿圈 |
mred按表2中一般外啮合的公式计算,有若干个行星轮时可按单个行星轮分别计算 |
内齿圈的当量质量可当作外齿轮处理 |
|||||||||||||||||||
|
表4 较特殊结构形式的齿轮的诱导质量mred |
|||||||||||||||||||||
|
齿轮结构形式 |
计算公式或提示 |
备 注 |
|||||||||||||||||||
|
1 |
小轮的平均直径与轴颈相近 |
采用表2一般外啮合的计算公式 因为结构引起的小轮当量质量增大和扭转刚度增大(使实际啮合刚度cγ增大)对计算临界转速nE1的影响大体上相互抵消 |
|
||||||||||||||||||
|
2 |
两刚性连接的同轴齿轮 |
较大的齿轮质量必须计入,而较小的齿轮质量可以略去 |
若两个齿轮直径无显著差别时,一起计入 |
||||||||||||||||||
|
3 |
两个小轮驱动一个大轮 |
可分别按小轮1-大轮 小轮2-大轮 两个独立齿轮副分别计算 |
此时的大轮质量总是比小轮质量大得多 |
||||||||||||||||||
|
4 |
中间轮 |
等效刚度
|
m1,m2,m3为主动轮、中间轮、从动轮的当量质量 cγ1-2——主动轮、中间轮啮合刚度 cγ2-3——中间轮、从动轮啮合刚度 |
||||||||||||||||||
|
表5 CV系数值 |
|||||||||||||||||||||
|
总重合度 系数代号 |
1<εγ≤2 |
εγ>2 |
|||||||||||||||||||
|
CV1 |
0.32 |
0.32 |
|||||||||||||||||||
|
CV2 |
0.34 |
|
|||||||||||||||||||
|
CV3 |
0.23 |
|
|||||||||||||||||||
|
CV4 |
0.90 |
|
|||||||||||||||||||
|
CV5 |
0.47 |
0.47 |
|||||||||||||||||||
|
CV6 |
0.47 |
|
|||||||||||||||||||
|
总重合度 系数代号 |
1<εγ≤1.5 |
1.5<εγ≤2.5 |
εγ>2.5 |
||||||||||||||||||
|
CV7 |
0.75 |
0.125sin[π(εγ-2)]+0.875 |
1.0 |
||||||||||||||||||
|
图1 系数CV1,…,CV7的数值 |
|||||||||||||||||||||
|
表6 |
|||||||||||||||||||||
|
Bp |
|
c'——单对齿轮刚度,见表齿轮刚度 Ca——沿齿廓法线方向计量的修缘量,μm,无修缘时,用由跑合产生的齿顶磨合量Cay(μm)值代替 fpbeff,ffeff——分别为有效基节偏差和有效齿廓公差,μm,与相应的跑合量yp,yf有关。齿轮精度低于5级者,取Bk=1 |
Cay |
当大、小轮材料相同时
|
|
||||||||||||||||
|
Bf |
|
当大、小轮材料不同时 Cay=0.5(Cay1+Cay2) |
Cay1、Cay2分别按上式计算 |
||||||||||||||||||
|
Bk |
|
fpbeff |
fpbeff=fpb-yp |
如无yp,yf的可靠数据,可近似取yp=yf=yα |
|||||||||||||||||
|
ffeff |
ffeff=ff-yf |
yα见表齿间载荷分配系数KHα、KFα中表1 fpb,ff通常按大齿轮查取 |
|||||||||||||||||||
|
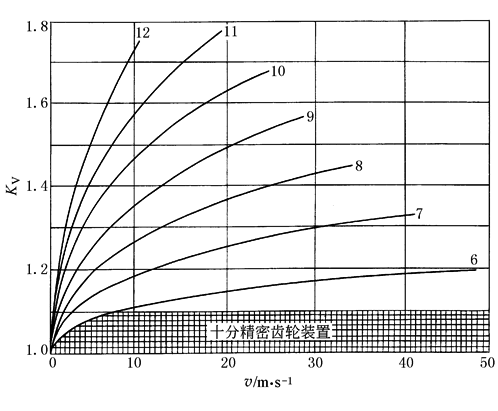
② 简化方法 KV的简化法基于经验数,主要考虑齿轮制造精度和节线速度的影响。KV值可由图2选取。该法适用于缺乏详细资料的初步设计阶段时KV的取值
图2 动载系数KV 注:6~12为齿轮传动精度系数。 对传动精度系数C≤5的高精度齿轮,在良好的安装和对中精度以及合适的润滑条件下,KV为1.0~1.1。C值可按表7中的公式计算 对其他齿轮,KV值可按图2选取,也可由表7的公式计算 |
|||||||||||||||||||||
|
表7 |
|||||||||||||||||||||
|
项 目 |
计 算 公 式 |
备 注 |
|||||||||||||||||||
|
传动精度系数C |
C=-0.5048ln(z)-1.144ln(mn)+2.852ln(fpt)+3.32 |
分别以z1、fpt1和z2、fpt2代入计算,取大值,并将C值圆整,C=6~12 |
|||||||||||||||||||
|
动载系数KV |
|
适用的条件 a.法向模数mn=1.25~50mm; b.齿数z=6~1200(当mn>8.33mm时, c.传动精度系数C=6~12 d.齿轮节圆线速度 |
|||||||||||||||||||