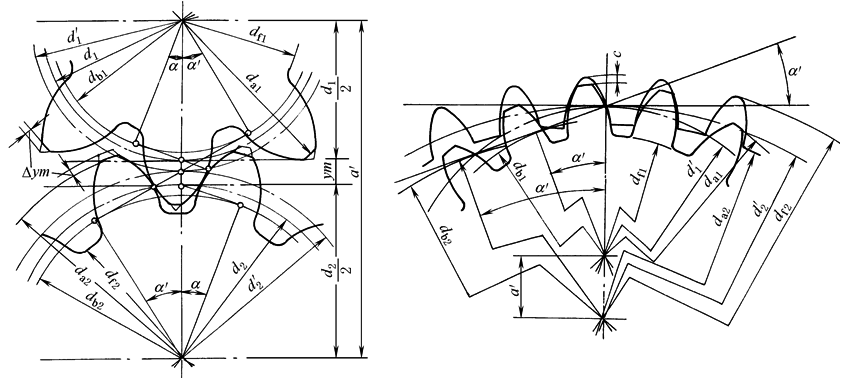
角变位齿轮传动的几何计算
项目				代号	计 算 公 式 及 说 明
					直齿轮(外啮合、内啮合)	斜齿轮(外啮合、内啮合)
分度圆直径				d	d1＝mz1 d2＝mz2
已 知 x 求 a'	啮合角			α'
					invα可由表渐开线函数invα＝tanα-α查出
	中心距变动系数			y
	中心距			a'
已 知 a' 求 x	未变位时的中心距			a
	中心距变动系数			y
	啮合角			α'
	总变位系数			x∑
					invα可由表渐开线函数invα＝tanα-α查出
	变位系数			x	x∑＝x2±x1	xn∑＝xn2±xn1
					外啮合齿轮变位系数的分配见表变位系数的选择方法
滚 齿	齿顶高变动系数			Δy	Δy＝(x2±x1)-y	Δyn＝(xn2±xn1)-yn
	齿顶高			ha
	齿根高			hf
	齿高			h	h1＝ha1+hf1 h2＝ha2+hf2	h1＝ha1+hf1 h2＝ha2+hf2
	齿顶圆 直径	外啮合		da	da1＝d1+2ha1 da2＝d2+2ha2	da1＝d1+2ha1 da2＝d2+2ha2
		内啮合			da1＝d1+2ha1 da2＝d2-2ha2 为避免小齿轮齿根过渡曲线干涉，da2应满足下式：	da1＝d1+2ha1 da2＝d2-2ha2 为避免小齿轮齿根过渡曲线干涉，da2应满足下式：
	齿根圆直径			df
插 齿	插齿刀参数			z0 x0 da0	按表直齿插齿刀的基本参数或根据现场情况选用插齿刀，并确定其参数z0、x0(或xn0)、da0，设计时可按中等磨损程度考虑，即可取x0(或xn0)＝0，da0＝m(z0+2ha0*)
	切齿时的啮合角			α'0
	切齿时的中心 距变动系数			y0
	切齿时的中心距			a'0
	齿根圆直径			df
	齿顶圆直径		外 啮 合	da
			内 啮 合		为避免小齿轮齿根过渡曲线干涉，da2应满足下式：	为避免小齿轮齿根过渡曲线干涉，da2应满足下式：
节圆直径				d'
基圆直径				db	db1＝d1cosα db2＝d2cosα	db1＝d1cosαt db2＝d2cosαt
齿顶圆压力角				αa
重 合 度	端面重合度			εα
					α(或αn)＝20°的εα可由下图查出
	纵向重合度			εβ	εβ＝0
	总重合度			εγ	εγ＝εα	εγ＝εα+εβ
当量齿数				zv
注：1.有“±”或“”号处，上面的符号用于外啮合，下面的符号用于内啮合。 2.对插齿加工的齿轮，当不要求准确保证标准的顶隙时，可以近似按滚齿加工的方法计算，这对于x＜1.5的齿轮，一般并不会产生很大的误差。 例1　已知外啮合直齿轮，α＝20°、ha*＝1、z1＝22、z2＝65、m＝4mm、x1＝0.57、x2＝0.63，用滚齿法加工，求其中心距和齿顶圆直径 (1)中心距 由表渐开线函数invα＝tanα-α查得α' ＝23°35' (2)齿顶圆直径 例2　例1的齿轮用z0＝25、ha0*＝1.25的插齿刀加工，求齿顶圆直径 插齿刀按中等磨损程度考虑，x0＝0，da0＝m(z0+2ha0*)＝4×(25+2×1.25)＝110mm 由表渐开线函数invα＝tanα-α查得α'01＝23°13' 由表渐开线函数invα＝tanα-α查得α'02＝21°59' 图1  端面重合度εα 注：1.本图适用于α(或αn)＝20°的各种平行轴齿轮传动。对于外啮合的标准齿轮和高变位齿轮传动，使用图2则更为方便。 2.使用方法：按α't和查出，按α't和查出，则，式中“+”用于外啮合，“-”用于内啮合。 3.α't可由图3查得。 图2  外啮合标准齿轮传动和高变位齿轮传动的端面 重合度εα(α＝αn＝20°、ha*＝han*＝1) 注：使用方法如下。 1.标准齿轮(ha1＝ha2＝mn)：按z1和β查出εα1，按z2和β查出εα2，εα＝εα1+εα2。 2.高变位齿轮[ha1＝(1+xn1)mn、ha2＝(1-xn1)mn]：按和β查出εα1，按和β查出εα2，εα＝(1+xn1)εα1+(1-xn1)εα2 图3  端面啮合角αwt(αP＝20°)