变位方式及变位系数的选择
在渐开线行星齿轮传动中，合理采用变位齿轮可以获得如下效果：获得准确的传动比、改善啮合质量和提高承载能力，在保证所需传动比前提下得到合理的中心距、在保证装配及同心等条件下使齿数的选择具有较大的灵活性 变位齿轮有高变位和角变位，两者在渐开线行星齿轮传动中都有应用。高变位主要用于消除根切和使相啮合齿轮的滑动比及弯曲强度大致相等。角变位主要用于更灵活地选择齿数，拼凑中心距，改善啮合特性及提高承载能力。由于高变位的应用在某些情况下受到限制，因此角变位在渐开线行星齿轮传动中应用更为广泛 常用行星齿轮传动的变位方法及变位系数可按下表及图1、图2和图3确定
常用行星齿轮传动变位方式与变位系数的选择
传动型式	高变位	角变位
NGW	1．＜4太阳轮负变位，行星轮和内齿轮正变位。即 -xA＝xC＝xB xA和xC按图1及图2确定	1．不等角变位 应用较广。通常使啮合角在下列范围： 外啮合：α'AC＝24°~26°30'(个别甚至达29°50') 内啮合：α'CB＝17°30'~21° 此法是在zA和zB不变，而将zC减少1~2齿的情况下实现的 这样可以显著提高外啮合的承载能力。根据初选齿数，利用图1预计啮合角大小(初定啮合角于上述范围内)；然后计算出xSAC、xSCB，最后按图2
	2．≥4　太阳轮正变位，行星轮和内齿轮负变位。即 xA＝-xC＝-xB xA和xC按图1及图2确定	2．等角变位 各齿轮齿数关系不变，即 zA+zC＝zB-zC 变位系数之间的关系为： xB＝2xC+xA 变位系数大小以齿轮不产生根切为准。总变位系数不能过大，否则影响内齿轮弯曲强度。通常取啮合角α'AC＝α'CB＝22° 对于直齿轮传动，当zA＜zC时推荐取 xA＝xC＝0.5
		3．当传动比时，推荐取α'AC＝24°~25°，α'CB＝20°，即外啮合为角变位，内啮合为高变位。此时， ×(zB-zC)式中，zC——齿数减少后的实际行星轮齿数
NW	1．内齿轮B及行星轮D采用正变位，即 xD＝xB 2．zA＜zC时，太阳轮A正变位，行星轮C负变位，即 xA＝-xC 3．zA＞zC时，太阳轮A负变位，行星轮C正变位，即 -xA＝xC 4．xA和xC按图1及图2确定	一般情况下：取αAC＝22°~27°和xSAC＞0 当zC＜zD时：取αDB＝17°~20°和xSDB≤0 当zC＞zD时：取αDB＝20°和xSDB≈0 用图1预计啮合角大小，确定各齿轮啮合副变位系数和，然后按图2
NGWN (Ⅰ)型	1．内齿轮E及行星轮D采用正变位，即 xD＝xE 2．当zA＜zC时： 如果zA＜17，太阳轮A采用正变位，行星轮C与内齿轮B采用负变位，即xA＝-xC＝-xB 如果zA＞17，太阳轮无根切危险时，因行星轮受力较大，行星轮不宜采用负变位，故不宜采用高变位传动 3．当zA＞zC时：太阳轮A负变位，行星轮C及内齿轮B正变位即-xA＝xC＝xB 4．xA和xC按图1和图2确定	1．zA+zC＝zB-zC＝zE-zD 由于未变位时的中心距aAC＝aCB＝aDE；啮合角α'AC＝α'CB＝α'DE。因此可采用非变位传动，亦可采用等角变位 2．zA+zC＜zB-zC＝zE-zD 由于未变位时的中心距aAC＜aCB＝aDE，则当zB＞zE时，建议取中心距a'＝a'CB＝a'DE。于是，a'AC＜a；则A-C传动即可实现xSAC＞0的变位。根据初选齿数，利用图1预计啮合角大小，然后计算出各对啮合副变位系数和。最后按图2 当zA＜zC时，C-B传动和D-E传动都不必变位 3．zA+zC＞zB-zC＝zE-zD 由于未变位时的中心距aAC＞aCB＝aDE，此时不可避免要使内齿轮正变位，而降低内齿轮弯曲强度(在NGWN传动中，由于内啮合副承担比外啮合副大得多的圆周力，故不宜使内齿轮正变位，仅在必要时，可取较小的变位系数)，因此一般较少用于重载传动。建议中心距a'＝aAC-(0.3~0.5)(aAC-aCB)。同样用图1预计啮合角大小，并确定各啮合副变位系数和，再按图2 4．zB-zC＜zA+zC＜zE-zD 可使D-E传动不变位或高变位；使A-C及C-B传动实现xSAC＞0及xSCB＞0的变位
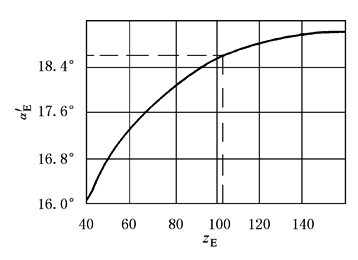
NGWN (Ⅱ)型		1．在一般情况下，内齿圈的变位系数推荐采用xE＝+0.25，而内齿圈E和B的顶圆直径按daE＝daB＝dE-1.4m＝(zE-1.4)m计算；行星轮C的顶圆直径daC应由A-C外啮合齿轮副的几何尺寸计算确定。以避免切齿和啮合传动中的齿廓干涉 2．C-E齿轮副啮合角的选取应使其中心轮A的变位系数为xA≈0.3 (1)当齿数差zE-zA为奇数，且变位系数xC＝xE＝+0.25时，可使xA≈0.3 (2)当齿数差zE-zA为偶数时，C-E齿轮副的啮合角α'E根据zE值由图3的线图选取可使xA≈0.3 (3)若允许中心轮A有轻微根切，则可取其变位系数xA＝0.20~0.25。当齿数差zE-zA为奇数和变位系数xC＝xE＝0.27~0.32时，可满足上述条件。此时C-E齿轮副的啮合角α'E＝20°，为高度变位
注：1．表中数值均指各传动型式中齿轮模数相同。 2．对斜齿轮传动，表中x为法向变位系数xn，α' 为端面啮合角。
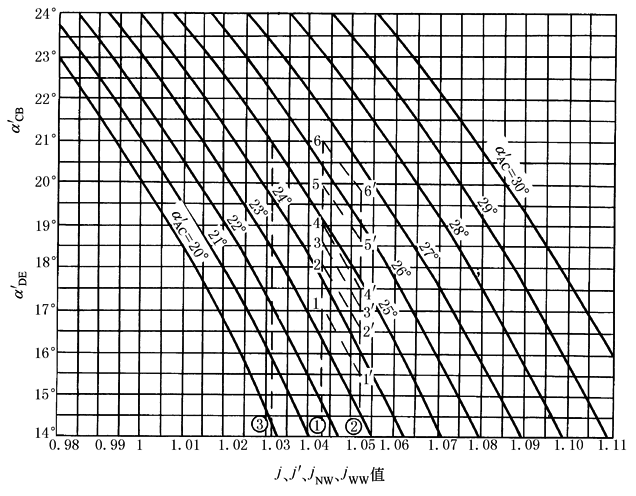
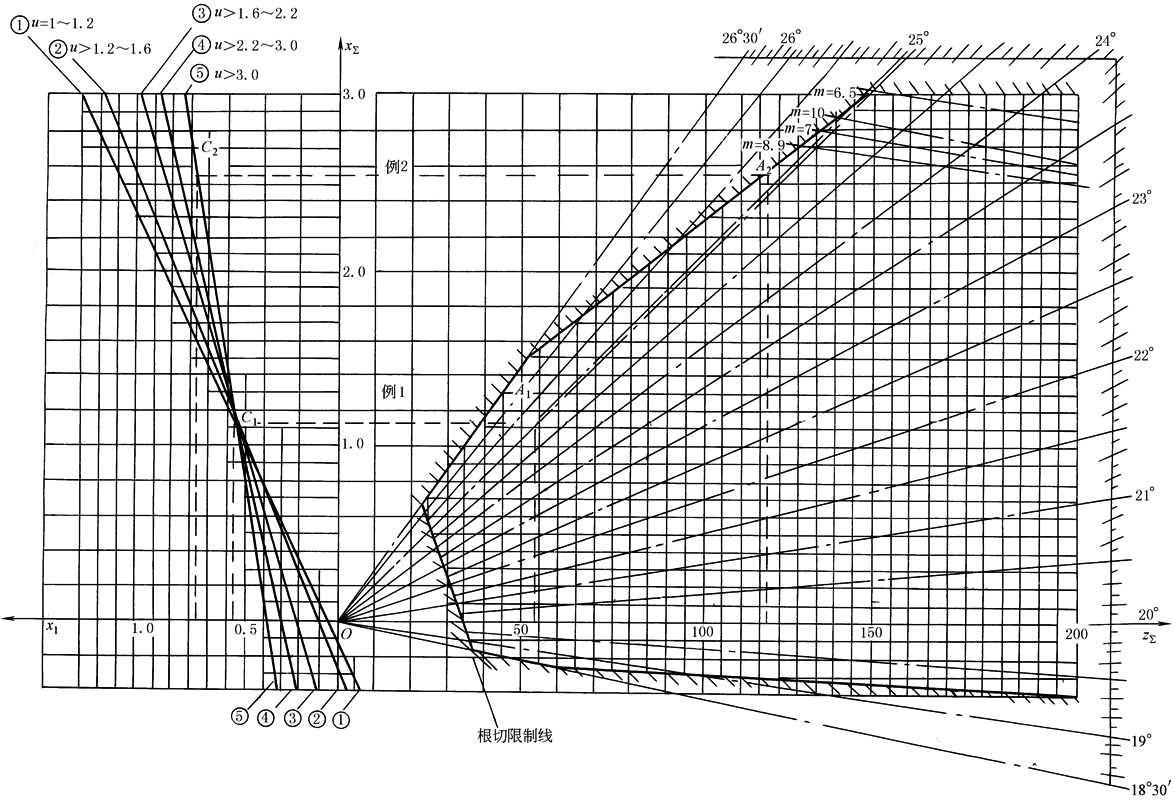
图1 变位传动的端面啮合角 (用于NGW型)；(连同 j 用于NGWN型)； (用于NW型)；(用于WW型) 图2 选择变位系数的线图(α＝20°，ha*＝1.0，u为齿数比，m为模数) 图3  确定NGWN(Ⅱ)型传动啮合角的线图 图1应用示例 例1　求j＝1.043的NGW型行星齿轮传动的啮合角α'AC、α'CB 解　在横坐标上取j＝1.043之①点，由①点向上引垂线，可在此垂线上取无数点作为α'AC与α'CB的组合，如1点(α'AC＝23°30'、α'CB＝17°)，…，6点(α'AC＝26°30'、α'CB＝21°)。从中选取比较适用的啮合角组合，如2~5点之间各点 例2　求j＝1.043、j'＝1.052的NGWN型行星齿轮传动的各啮合角组合 解　先按j值及j'值由①点和②点分别做垂线，①点的垂线上，1，2，…，6的对应点为②点垂线上的1'，2'，…，6'。从而得啮合角组合，如1—1'(α'AC＝23°30'、α'CB＝17°、α'DE＝15°20')…6—6'(α'AC＝26°30'、α'CB＝21°、α'DE＝19°45')等无数个啮合角组合，从中选取比较合适的啮合角组合，如可选α'AC＝26°、α'CB＝20°25'、α'DE＝19°的啮合角组合 例3　求jNW＝1.031的NW型行星齿轮传动的啮合角组合 解　按jNW值在横坐标上找到③点，由③点向上做垂线，从垂线上无数点中选取比较合适的啮合角组合，如α'AC＝24°15'、α'DE＝20°的一点 图2应用示例 已知：一对齿轮，齿数z1＝21，z2＝33，模数m＝2.5mm，中心距a'＝70mm。确定其变位系数 解　1) 根据确定的中心距a' 求啮合角α' 2) 图2中，由O点按α'＝25°01'25"作射线，与zS＝z1+z2＝21+33＝54处向上引垂线，相交于A1点，A1点纵坐标即为所求总变位系数xΣ(见图中例，xΣ＝1.12)。A1点在线图许用区内，故可用 xΣ也可根据α' 按无侧隙啮合方程式求得 3) 根据齿数比，故应按该图左侧的斜线2分配变位系数，即自A1点作水平线与斜线2交于C1点：C1点的横坐标x1＝0.55，则x2＝xΣ-x1＝1.12-0.55＝0.57